Today on my blog there's a novelty - a guest post. I'm already so lazy to write that I'm making other people do it. What won't you do to make you have fun. Basically, please love and favor - Masha. She went to a couple of interviews, and apparently, she liked it more than everyone :D The floor is hers.
Hi everyone! I was at an interview at one large company that hires only Russian speakers even for technical positions. Why? Don't know.
So, imagine my surprise when math problems made up a third of all questions. Some of them were elementary for everyone, some - elementary for those who finished school. I won't name the company, but for the curious I'll break down the problems I encountered there.
So, the first problem goes by the code name "problem about the equator". Simple, but the main thing is not to be lazy and get a numerical answer. It sounds like this: "Suppose that Earth is absolutely round, and we stretched a rope along its equator without a gap (for especially meticulous - the gap value can be neglected). Question: will a person be able to walk under the rope if the rope length is increased by 10 meters?". Next will follow the answer, so if you want to think, stop HERE.
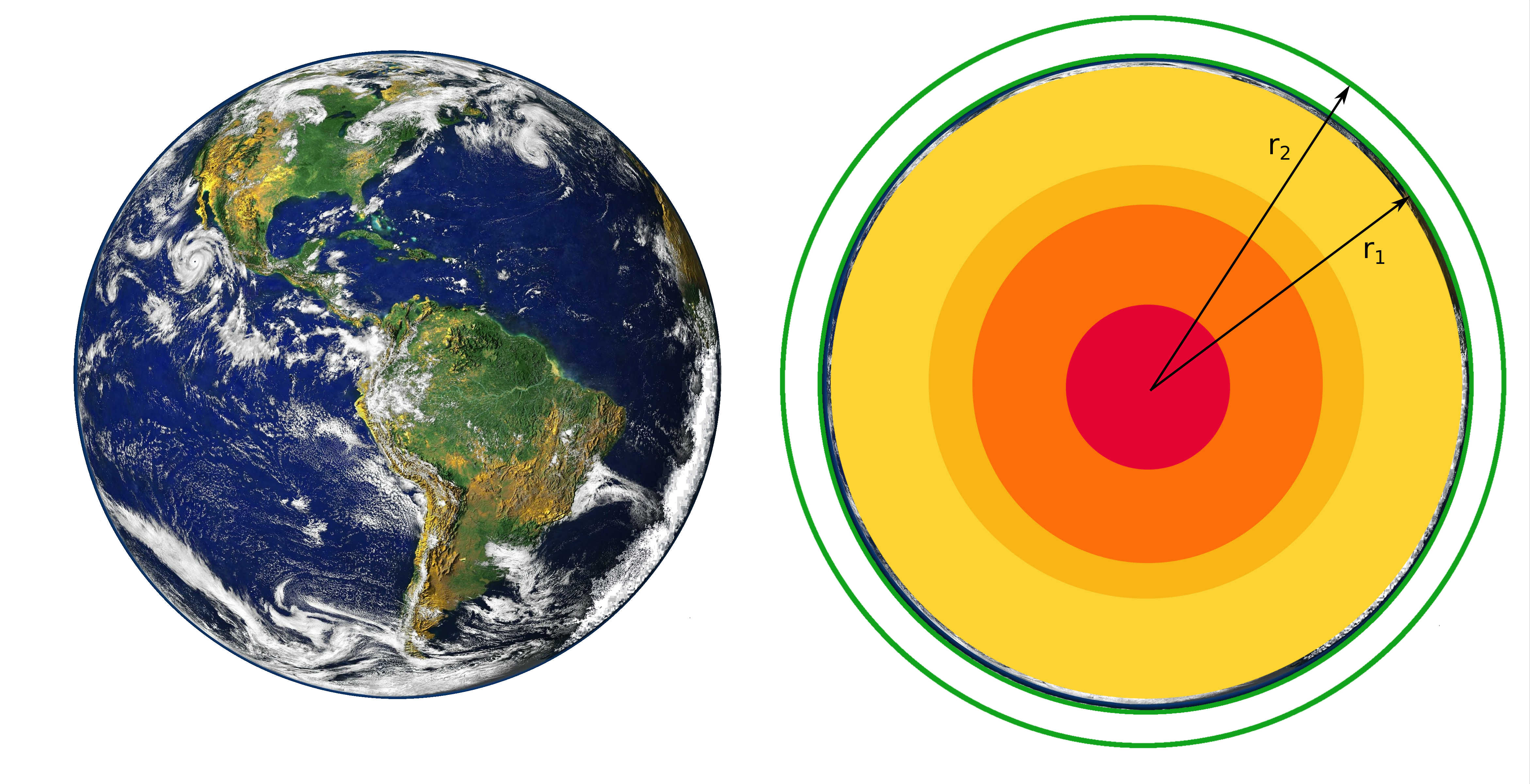
Here we need to compare radius r1 and r2. Well, I think everyone remembers the formula for circle length learned forever l = 2πr. Well, now let's write the length of a circle with radius r2: l1 + 10 = 2πr2. From here, r2 = (2πr1+10)/(2π) and r2 = r1+10/(2π)= r1 + 1.59 meters. In other words, the difference between these two radii is 1.59 meters and a person will quite easily walk under the rope.
Second problem, I call it "biological": "A bacteria divides in half once per 1 second. If you put 1 such bacteria in a jar, then in exactly one minute the whole jar will be filled with bacteria. Question: in what time will the jar be filled by 1/8?".

Again, everything is very simple. If every second the number of bacteria doubles, then at 59 seconds the jar was filled halfway, at 58 seconds - by 1/4, and at 57 seconds - by 1/8.
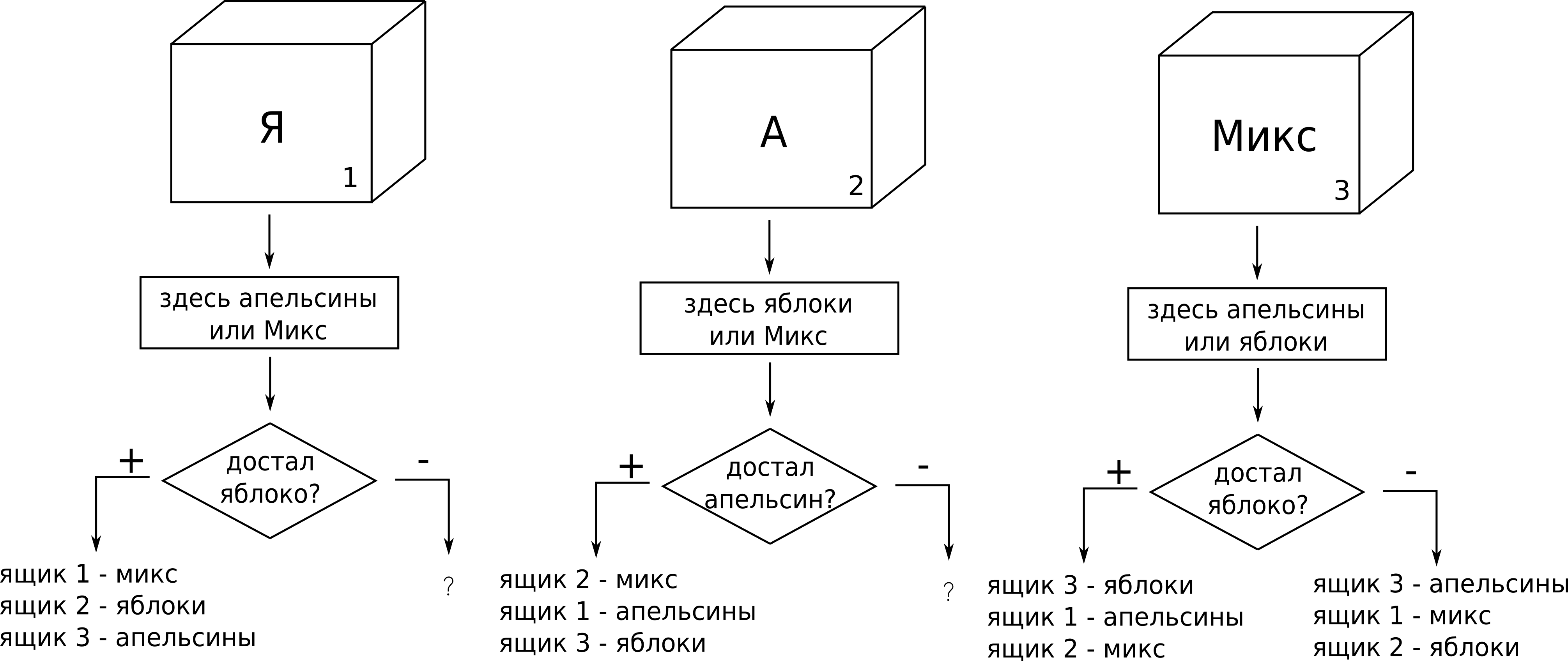
Third problem about "boxes": "There are three boxes. In one lie apples, in another - oranges, in the third - apples and oranges. On each of them it's written what's inside, but all these inscriptions are incorrect. Is it possible by taking out one fruit from any box to accurately determine which box contains what?". Answer in the picture:
Well, and finally the problem "about squirrels": "One and a half squirrels eat one and a half nuts in one and a half hours. How many nuts will 9 squirrels eat in 9 hours?". Here I leave room for your imagination.
If the problem seemed easy, here's an additional question for you: "In what case could it happen that we have data on the number of nuts eaten by one and a half squirrels (after all, we all understand that the math teacher wouldn't praise us for such a problem)? " Unfortunately, I don't know the answer to this question and can only guess.
Basically, as you already understood, Masha sat in the first row in math class. If you liked the article, I advise visiting her blog too, where she writes about mathematics (as she thinks) for simple people (as she thinks) :D
Masha's Learning - blog about mathematics.